Convolution of PDF: 2つの確率変数の和の分布を求める
本ページでは、確率変数$X,Y$について、$X+Y=Z$の確率密度関数(Probability Density Function)の導出方法と具体例を示す。 ただし、以下を前提とする。
- $X,Y$は互いに独立である
- $X,Y$の確率密度関数は既知であり、それぞれ$f_X\left(x\right),f_Y\left(y\right)$である
導出方法
導出手法には、解析的、数値的の2種類のアプローチがある。 解析的アプローチが難しい場合に、数値的アプローチを選択することが一般的である。
解析的導出
$X+Y=Z$の確率密度関数$f_Z\left(z\right)$は、以下のように畳み込みで求めることができる。
$$ f_Z\left(z\right) = \int^{\infty}_{-\infty} f_X\left(x\right)f_Y\left(z-x\right) dx $$
数値的導出
積分が困難な場合は、モンテカルロ法を使う。
導出例
| $f_x\left(x\right)$ | $f_y\left(y\right)$ | $f_z\left(z\right)$ | |
|---|---|---|---|
| 正規分布: $\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2}\right)$ | 指数分布: $\lambda \exp\left(-\lambda x\right)$ | ExGaussian: $\lambda \exp\!\left( \lambda\mu + \frac{1}{2}\lambda^2\sigma^2 - \lambda z \right)\cdot \tfrac{1}{2}\, \mathrm{erfc}\!\left( \frac{\mu + \lambda\sigma^2 - z}{\sqrt{2}\,\sigma} \right)$ | 導出手順 |
1. 正規分布+指数分布
畳み込みは以下の式によって行う。 ただし、指数分布の定義域より、$z-x \geq 0$であるため、積分範囲は$\left[-\infty,z\right]$となる。
$$ \begin{split} f_Z\left(z\right)&=\int^{\infty}_{-\infty} f_X\left(x\right)f_Y\left(z-x\right) \\ &=\int^{z}_{-\infty} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2}\right) \cdot \lambda \exp\left(-\lambda \left(z-x\right)\right) dx \\ &=\frac{\lambda}{\sqrt{2\pi\sigma^2}}\exp\left(-\lambda z\right)\int^{z}_{-\infty}\exp\left(\lambda x-\frac{\left(x-\mu\right)^2}{2\sigma^2}\right)dx \end{split} $$
ここで、被積分項の$\exp$の中身を平方完成する。
$$ -\frac{\left(x-\mu\right)^2}{2\sigma^2}+\lambda x = -\frac{1}{2\sigma^2}\left(x-\alpha\right)^2 + \frac{\alpha^2-\mu^2}{2\sigma^2}, \alpha=\mu+\sigma^2\lambda $$
平方完成の結果を使うと、$f_Z\left(z\right)$は以下のように表せる。
$$ f_Z\left(z\right)=\frac{\lambda}{\sqrt{2\pi\sigma^2}}\exp\left(-\lambda z + \frac{\alpha^2-\mu^2}{2\sigma^2}\right)\int^{z}_{-\infty}\exp\left(-\frac{\left(x-\alpha\right)^2}{2\sigma^2}\right)dx $$
$u=\frac{x-\alpha}{\sqrt{2}\sigma}$として置換積分を行う。
$$ dx=\sqrt{2}\sigma du, x=z \implies u=\frac{z-\alpha}{\sqrt{2}\sigma} \\ \begin{split} \int^{z}_{-\infty}\exp\left(-\frac{\left(x-\alpha\right)^2}{2\sigma^2}\right)dx &= \sqrt{2}\sigma \int^{\frac{z-\alpha}{\sqrt{2}\sigma}}_{-\infty} e^{-u^2}du \\ &= \sqrt{2}\sigma \int^{\infty}_{\frac{\alpha-z}{\sqrt{2}\sigma}} e^{-u^2}du \\ &= \sigma\sqrt{\frac{\pi}{2}}\mathrm{erfc}\left(\frac{\alpha-z}{\sqrt{2}\sigma}\right) \end{split} $$
以上より、$f_Z\left(z\right)$は誤差関数$\mathrm{erfc}\left(x\right)$あるいは正規分布の累積分布関数$\Phi\left(x\right)$を用いて以下のように表せる。 この確率密度関数で表される分布は、ExGaussian分布と呼ばれる。
$$ \begin{split} f_Z\left(z\right) &= \frac{\lambda}{2}\exp\left(-\lambda z + \frac{\alpha^2-\mu^2}{2\sigma^2}\right) \mathrm{erfc}\left(\frac{\alpha-z}{\sqrt{2}\sigma}\right) \\ &= \lambda\exp\left(\lambda \mu+\frac{\lambda^2\sigma^2}{2}-\lambda z\right) \cdot \frac{1}{2}\mathrm{erfc}\left(\frac{\mu+\sigma^2\lambda-z}{\sqrt{2}\sigma}\right) \\ &= \lambda\exp\left(\lambda \mu+\frac{\lambda^2\sigma^2}{2}-\lambda z\right) \cdot \Phi\left(\frac{z-\mu}{\sigma}-\lambda \sigma\right) \end{split} $$
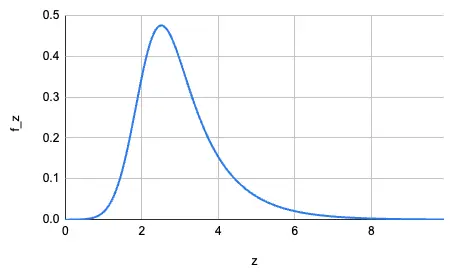
ちなみに、$f_Z\left(z\right)$のグラフは下図の通り。 ちょっと左に偏った正規分布っぽい感じになる。